How to achieve industrial process improvement? Is there some scientifically recognized methodology for this purpose? What are the most commonly used software tools for this purpose? Is there a place for BRUTOMIZER?
These are the questions I am going to try to answer in this post.
To effectively apply production technology for a particular task on a particular machine is far from a trivial problem. Determination of the suitable set of machine’s main parameters which are supposed to govern the process itself is a delicate task, but extremely important. The importance and possible repercussions of this task are often overlooked, even in big production companies.
In production companies, it is common practice that machine operators and/or process planning engineers select the suitable set of the machine’s main parameters based on acquired knowledge and experience, handbooks, and guidelines. Although this is essentially a subjective approach, and selected parameters are not even near-optimal ones, in most cases, this approach may be sufficient.
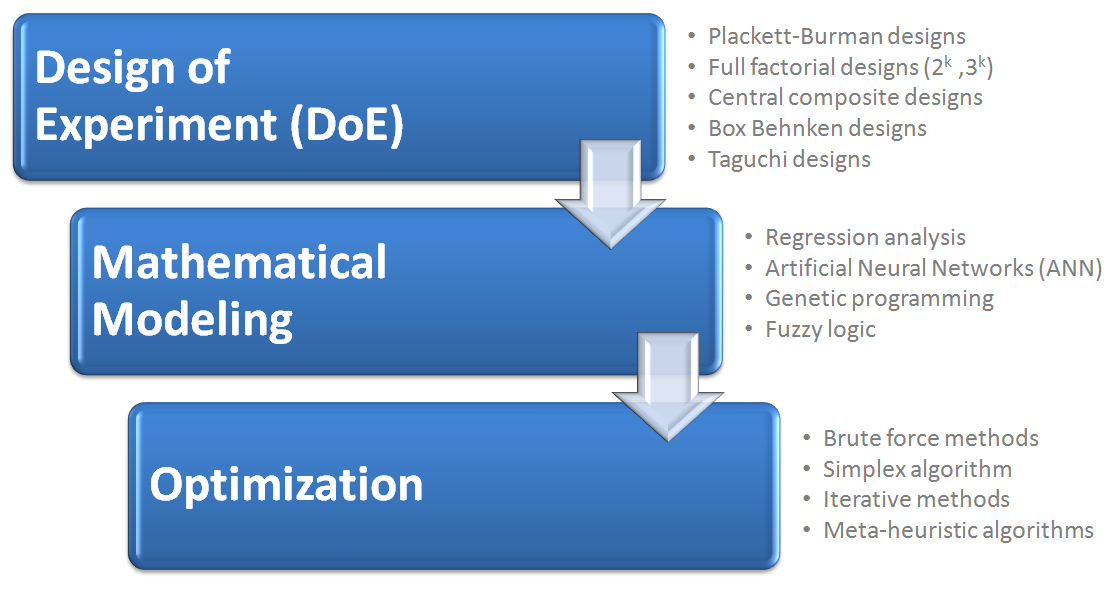
However, there are cases when there is a need to produce a large number of parts, use expensive raw materials, use raw materials or tools from different suppliers, produce finished parts from the limited amount of available workpiece material, or finally experience any novel situation. In these cases, comprehensive analysis and detailed process planning for the selection of the machine’s main parameters are necessary and preferred. The situation is even more complex when attempting to satisfy multiple performance characteristics – objectives (to maximize productivity, to minimize cost, to decrease any types of defects, etc.). It is almost a general rule for any production technology that the set of machine’s main parameters which is most suitable for one performance characteristic may deteriorate other performance characteristics. In that sense, in order to ensure the achievement of the required quality, cost minimization, and productivity maximization, it is necessary to quantify the relationships between the main parameters that govern the given process and process performance characteristics. This is accomplished through a scientifically recognized three-step procedure: (1) experimentation with the use of DoE techniques, (2) mathematical modeling, and (3) optimization.
Design of experiments (DoE)
Each process optimization starts with an experiment. It is logical to say that the more experiment trials we have the better. But at the same time, we do not want to spend too much time or resources on experimenting. DoE methods help engineers select only the most important experiment trials, and still gain maximal amount of information out of it.
DoE is in fact a set of statistical and mathematical methods for planning, realization, analysis, and interpretation of experimental trials and results in order to: identify the main control parameters of the given process, develop mathematical models that describe the given process, and finally set the basis for process optimization. By using scientific principles of DoE methods, one uses a minimal number of experimental trials along with minimal time and material expenses and at the same time ensures maximization of gained information. It should be noted that DoE uses a cybernetic principle of “black box”, thus it can be applied to every process and system.
Mathematical modeling
After collecting experiment results, we want to get some correlation between inputs and outputs. Mathematical modeling aims at establishing mathematical relations, in the form of equations, between outputs (dependent variables, performance characteristics, objective functions) and inputs (independent variables, factors used in DoE) by using the obtained experimental data. Previous research from theory and practice has shown that mathematical models in the form of a polynomial (linear, quasi-linear, and quadratic) are the most convenient. The potential application of the developed model is valid only in the covered experimental hyperspace, which is defined in the DoE stage. It should be noted that the selection of the most suitable mathematical model is often more art than science, and the final selection must incorporate other aspects related to the process being modeled.
Optimization
Optimization aims to identify an optimal solution – minimum or maximum of outputs (dependent variables, performance characteristics, objective functions) and corresponding inputs. Finding the optimal or near-optimal solutions of the objective function with or without constraints is quite a complex task because the mathematical models of given processes may be complex, multidimensional, and nonlinear. With optimized processes one can expect increased productivity, decreased production cost, improved quality, reduced waste, and overall increased profit.
Why use BRUTOMIZER?
Application of DOE, mathematical modeling and optimization techniques for process optimization have been well-recognized by a number of companies across the world. A number of real case studies from different industries confirm the validity and effectiveness of the applied approach. There are many powerful and expensive software solutions developed by big software companies such as MINITAB, DOE++, Design-Expert, JMP, MATLAB, Mathematica, Quantum XL 2016, etc. These software solutions offer a broad spectrum of methods and algorithms but require expert knowledge to select which method to use for a specific problem. Furthermore, a selected method often has many parameters that should be adjusted, which also requires expert knowledge.
Our goal when developing BRUTOMIZER was not to develop a comprehensive software tool that covers the complete three-step methodology. Instead, it covers only a small subset of the third step – optimization.
BRUTOMIZER is intended for solving constrained/unconstrained optimization problems that use empirical mathematical models. A number of real case studies from industrial practice indicate that empirical mathematical models that cover up to 6-dimensional experimental hyperspace are practical and useful. Therefore it is sufficient to use the brute force algorithm which is implemented in BRUTOMIZER for the purpose of optimization as this approach guarantees the optimality of the obtained solutions.
In contrast to existing solutions, BRUTOMIZER offers:
- Simple mathematical model definition, WITHOUT the need to write any code
- Simple formulation of optimization problems with or without constraints
- Simple definition of independent variables range and possible step for each variable
- Simple optimization methods based on brute force search, WITHOUT any parameters to set
- Ability to determine a specified number of solutions: in the case of maximization, minimization, or in the case of targeting specified function value
The two most important practical benefits of the use of BRUTOMIZER are:
- GUARANTEED OPTIMALITY of the obtained solutions
- obtained optimal solution inputs can READILY be set on the machine
Obviously, BRUTOMIZER is not developed to replace the aforementioned existing software tools. But in some cases, it can be easier and more convenient to use BRUTOMIZER for the final step of optimization, as any mathematical model, including mathematical models obtained in other software tools (i.e. MATLAB, MINITAB, etc.), can easily be defined in BRUTOMIZER.